4.2. Анализ схем на переменном токе
Упражнения
Методические указания В этом разделе представлены упражнения по расчету и пошаговой экспериментальной проверке его результатов на Electronics Workbench для схем, содержащих один источник гармонического сигнала и разветвленную пассивную часть. Традиционным методом решения таких задач является метод свертки-развертки схемы. Вычисления при этом должны выполняться в комплексной форме с применением соответствующего калькулятора. Для вычислений с комплексными числами мы рекомендуем простую программу Comcal, описание которой приведено в приложении 2 и в рассмотренном примере решения (задача 1) показано применение этой программы. Electronics Workbench позволяет проводить пошаговую проверку результатов расчета путем соответствующих измерений. На каждом шаге расчета мы получаем комплексное сопротивление или комплексы тока и напряжения, которые могут быть измерены косвенно с помощью осциллографа или непосредственно с помощью Боде-плоттера (методика таких измерений изложена в приложении 1). В другом примере (задача 2) иллюстрируется применение метода пропорциональных величин для расчета линейных схем. Метод позволяет установить все амплитудно-фазо-вые соотношения по отношению к току или напряжению выбранного элемента при произвольно заданной их величине. Обычно расчет доводят до вычисления параметров входного источника энергии. Очевидно, что изменение амплитуды источника приведет к пропорциональному изменению амплитуд всех векторов, а изменение его фазы — к повороту всей диаграммы на угол, равный этому изменению. Задача 1. Расчет схемы, методом свертки
Задание: В схеме рис. 4.11 определить методом свертки-развертки комплекс тока через сопротивление Ri и вычислить полную мощность источника питания в комплексной форме записи. ФайлСЗ_07. са4, рис. 4.11 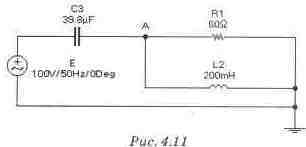
Порядок расчета
Шаг 1. Рассчитывается реактивное сопротивление катушки
индуктивности Х2.
Шаг 2. Рассчитывается эквивалентное комплексное сопротивление
Z12 двух параллельных ветвей Х2 и R1.
Шаг 3. Рассчитывается полное сопротивление пассивного
двухполюсника нагрузки Z123.
Шаг 4. Вычисляется ток 13 через конденсатор СЗ.
Шаг 5. По формуле делителя тока вычисляется ток IR1
Расчет
Текст из программы комплексного калькулятора с результатами
!
Расчет схемы из трех пассивных элементов с одним
источником !
Исходные данные F=50 R1-60 L2=0.2 03=0.0000398 Е=100
!
Определить токи и напряжения для всех компонентов
!
Найти полную, активную и реактивную мощности !
Расчет проведем методом свертки-развертки Результат
операции вместе с текстом ее мы будем отражать в таблице. !
Определяем входное сопротивление методом свертки
В разделе 3.2 мы использовали для расчетов с действительными числами только одно табло для вывода результата (Real). Однако в данной задаче расчет должен вестись уже над полем комплексных чисел и для информации о результате используются еще четыре табло: мнимая часть (Imag), модуль числа (Abs), аргумент в радианах (Arg, рад) и в градусах (Arg, rp). tiapuc. 4.12 табло представляют результат вычисления комплекса Z123. Положение курсора (серая полоса на. рис. 4.12) показывает, что вычисляется именно эта величина.
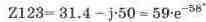

Экспериментальная проверка результатов расчета Для экспериментальной проверки правильности вычислении необходимо измерить комплексное сопротивление пассивной части цепи. В показательной форме записи комплексное сопротивление характеризуется двумя величинами: модулем и фазой, каждая из них должна измеряться в отдельности. Учитывая, что комплексное сопротивление двухполюсника равно отношению комплекса напряжения к комплексу тока, можно предложить следующую методику экспериментального измерения: подключить на вход цепи источник тока с действующим значением 1 А и нулевой начальной фазой и измерить комплекс напряжения на зажимах двухполюсника, величина которого и будет численно равна комплексному сопротивлению. Таким образом мы свели задачу к измерению комплекса напряжения. Проще всего измерить параметры, составляющие комплекс при записи его в показательной форме: модуль и фазу. Модуль измеряется обычным вольтметром действующих значений, а фаза осциллографом. Однако более рационально измерение комплекса напряжения с помощью Боде-плоттера. Схема такого измерения представлена на рис. 4.13. Схема для экспериментальной проверки шагов 1..3 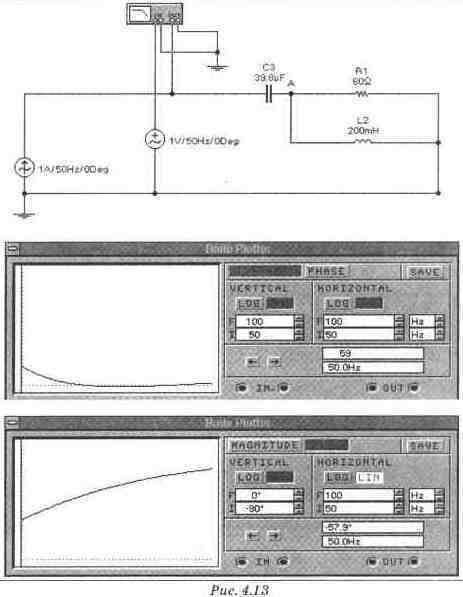
Расчет Текст из программы комплексного калькулятора с результатами .' Определяем ток источника питания
|
Операция |
Real |
Imag |
Abs |
Arg, гр |
|
I3=E/Z123 |
0.9 |
1.435 |
1.694 |
-58 |
Экспериментальная проверка результатов расчета Схема для экспериментальной проверки шага 4 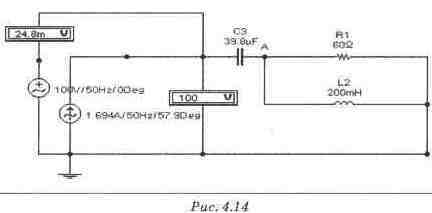
Идея экспериментальной проверки правильности расчета тока источника питания заключается в следующем: а). На вход схемы рис. 4.14 подключается источник тока с вычисленными на шаге 4 параметрами; б). Напряжение на входе схемы сравнивается с заданным в условии напряжением источника питания. Вольтметр, включенный последовательно с источником ЭДС, оценивает ошибку расчета. Шаги 5. 6,7, 8, 9
Расчет Текст из программы комплексного калькулятора с результатами / Определяем токи через параллельные ветви по формуле делителя тока
|
Операция |
Real |
Imag |
Abs |
Arg,rp |
|
I2=I3*R1/(R1+X2) |
1.146 |
0.234 |
1.169 |
11.5° |
|
I3=E/Z123 |
0.9 |
1.435 |
1.694 |
-58' |
/ Определяем потенциал узлаА
|
Операция |
Real |
Imag |
Abs |
Arg,гр |
|
UA= I1*R1 |
-14.74 |
72 |
73.5 |
101.5 |
' Определяем комплекс мощности 
Экспериментальная проверка результатов расчета Схема для экспериментальной проверки шагов 5, 6, 7, 8 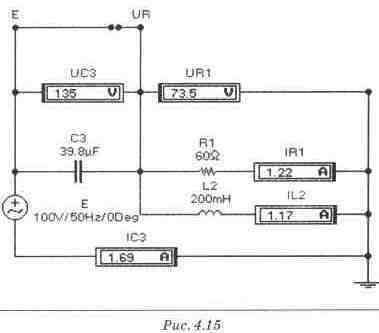
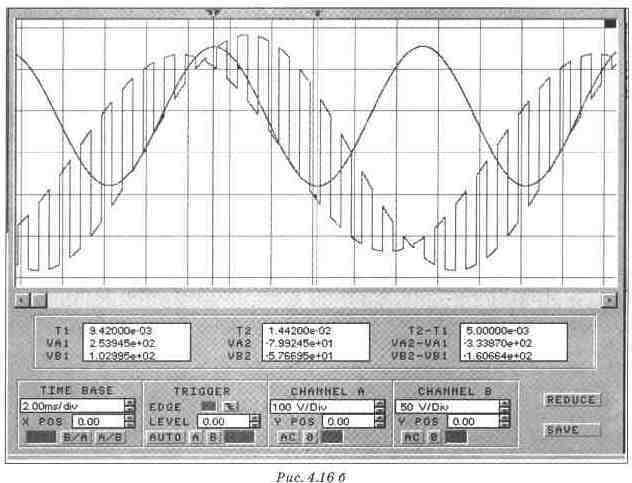
Схема для получения осциллограмм мгновенной мощности источника питания (рис. 4.16а, б) 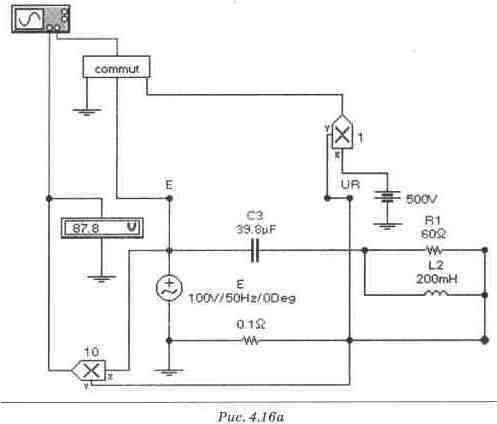
Задача 2. Применение метода пропорциональных величин для расчета схем
Задание: Для схемы рис. 4.17 определить напряжение на входе, если ток 14 равен 4А. Расчет сопровождать построением топографической векторной диаграммы напряжений и векторной диаграммы токов. Файл с4_08. 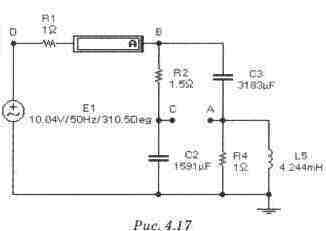
Порядок расчета и построения векторной диаграммы
Шаг 1. Вектор 14 направляем по действительной оси.
По заданному току 14 определяем напряжение UA. Строим вектор UA.
Шаг 2. По напряжению UA определяем ток 15. Строим
вектор 15.
Шаг 3. На основании 1 закона Кирхгофа для узла А
вычисляем ток 13. Строим вектор 13. Проверяем полученные соотношения экспериментально.
Шаг 4. Вычисляем напряжение UAB. На основании второго
закона Кирхгофа определяем напряжение UB. Строим вектор UB.
Шаг 5. Определяем вектор тока 12. Вычисляем напряжение
UBC. На основании второго закона Кирхгофа определяем напряжение UC. Строим вектор
UC.
Шаг 6. На основании 1 закона Кирхгофа для узла А
вычисляем ток I1. Строим вектор I1.
Шаг 7. Вычисляем напряжение UCD. На основании второго
закона Кирхгофа определяем напряжение UD. Строим вектор UD.
Шаги 1,2и 3
Расчет и построение векторных диаграмм Расчет проведем, предположив, что ток через сопротивление R4 имеет нулевую фазу, вектор тока на комплексной плоскости направлен по действительной оси. Вычисления будем проводить в программе комплексного калькулятора (файл сЗ_8.сс), текст которого будем приводить по ходу решения вместе с результатами расчета. Текст из программы комплексного калькулятора с результатами ! Расчет схемы сложной схемы с одним источником ! Исходные данные F=50 R1=1 R2=1.5 С2=0.001591 С3=0.003183 R4=l L5=0.004244 14=4 ! 1. Напряжение на R4
|
Операция |
Real |
Imag |
Abs |
Arg, rp |
|
U4=I4*R4 |
4.0 |
|
|
|
.' 2. Ток через ветвь L5
|
Операция |
Real |
Imag |
Abs |
Arg,rp |
|
Х5^*2*р*Г*Ь5 |
|
1.333j |
|
|
|
I5=U4 / Х5 |
|
-3j |
|
|
! 3. Первый закон Кирхгофа для узла А
|
Операция |
Real |
Imag |
Abs |
Arg, rp |
|
13=14+15 |
4 |
-3-j |
5 |
-З7 |
Поскольку напряжение на резисторе совпадает по направлению с током, вектор напряжения U4 также направлен по действительной оси (рис, 4,186). Ток же через катушку индуктивности 15 должен отставать от напряжения на ней на 90 (рис. 4.18а). Первый закон Кирхгофа для узла А графически отражается прямоугольным треугольником токов (рис. 4.18а). Прямоугольный треугольник токов отражает первый закон Кирхгофа для параллельного соединения активного и реактивного сопротивлений.
Векторные диаграммы 
Экспериментальная проверка результатов расчета Схема для экспериментальной проверки шагов 1..3 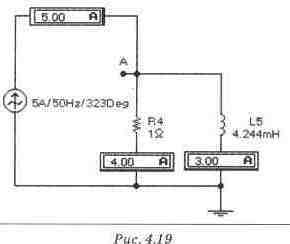
Для экспериментальной проверки этой части расчета
достаточно к узлу А подключить источник тока, действующее значение и фаза которого
совпадают с вычисленными значениями для комплекса 13, и проверить действующие
значения токов в ветвях. Как видно из рис. 4.19, и действующие значения, и фаза
суммарного тока совпадают с расчетными.
Шаг 4
Расчет и построение векторных диаграмм для схемы рис. 4.21 Текст из программы комплексного калькулятора с результатами ' 4. Второй закон Кирхгофа для потенциала узла В
|
Операция |
Real |
Imag |
Abs |
Arg, rp |
|
ХЗ—1*1/(2*р*F*СЗ) |
|
-j' |
|
|
|
UBA=I3*X3 |
-35 |
4.j |
5 |
-127 |
|
UB=U4+UBA |
1 |
-4j |
4.123 |
-76" |
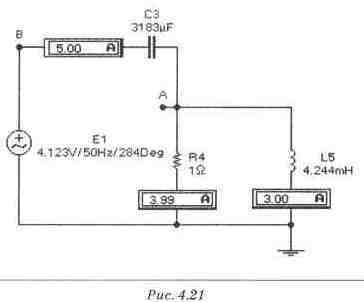
Векторные диаграммы 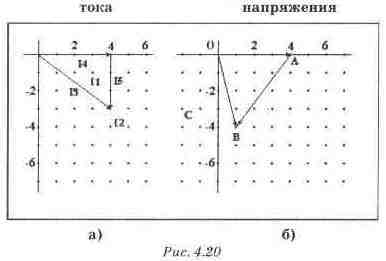
Вектор напряжения на емкостном сопротивлении ХЗ по правилам построения топографической диаграммы напряжений мы должны построить из конца вектора напряжения на R4. Кроме того, он должен отставать от вектора тока 13 на 90° (рис. 4.206). По второму закону Кирхгофа потенциал UB=U4+UBA. Второй закон для последовательной цепи из трех участков графически отражается треугольником ОАВ (рис. 4.206). Экспериментальная проверка результатов расчета Для экспериментальной проверки этой части расчета достаточно к узлу В подключить источник напряжения, действующее значение и фаза которого совпадают с вычисленными значениями для комплекса UB, и проверить действующие значения токов в ветвях. Как видно из рис. 4.21, при действующем значении и фазе напряжения UB, совпадающих с расчетными, токи имеют вычисленные значения. Схема для экспериментальной проверки шага 4
Шаг 5
Расчет и построение векторных диаграмм Текст из программы комплексного калькулятора с результатами ! 5.Ток для ветви R2-C2 (рис. 4.17)
|
Операция |
Real |
Imag |
Abs |
Arg,rp |
|
X2=-j/(2*p*F*C2) |
|
-2j |
|
|
|
Z2=R2+X2 |
1.5 |
-2j |
2.5 |
-53' |
|
I2=UB/Z2 |
1.52 |
-0.64j |
1.65 |
-23 |
Поскольку вектор UR2 совпадает по направлению с вектором 12, а вектор UC2 должен отставать от него на 90, второй закон Кирхгофа для RC-ветви отображается графически прямоугольным треугольником (рис. 4.226}. Векторные диаграммы 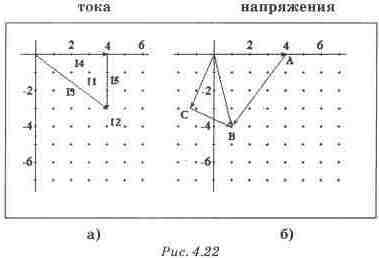
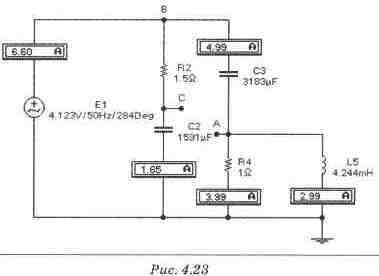
Экспериментальная проверка результатов расчета Для экспериментальной проверки этой части расчета необходимо к узлу В подключить ветвь R2—C2 и проверить действующие значения тока в ней. Как видно из рис. 4.23, оно совпадает с вычисленным. Схема для экспериментальной проверки шага 5 (см. рис. 4.23) Шаги 6 и 7
Расчет и построение векторных диаграмм Текст из программы комплексного калькулятора с результатами .' 6. Потенциал узла С (рис. 4.17)
|
Операция |
Real |
Imag |
Abs |
Arg,rp |
|
UC=I2*X2 |
1.28 |
-3.04-j |
3.3 |
-113' |
! 7. Первый закон Кирхгофа для узла В
|
Операция |
Real |
Imag |
Abs |
Arg, rp |
|
11=12+13 |
5.51 |
-3.64j |
6.61 |
-33° |
Векторные диаграммы 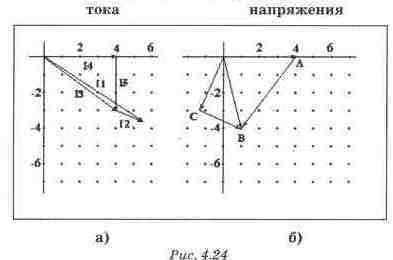 s
s
Экспериментальная проверка результатов расчета Для экспериментальной проверки этой части расчета необходимо к узлу В подключить вольтметр к конденсатору С2 и амперметр в цепь питания, проверить действующие значения тока и напряжения. Как видно из рис. 4.23, они совпадают с вычисленными. Схема для экспериментальной проверки шагов 6 и 7 (см. рис. 4.25) Шаг 8
Расчет и построение векторных диаграмм Текст из программы комплексного калькулятора с результатами 8. Второй закон Кирхгофа для потенциала узла D
|
Операция |
Real |
Imag |
Abs |
Arg, гр |
|
UBD=I1*R1 |
5.51 |
-3.64j |
6.61 |
-33 |
|
UD=UB+UBD |
5.51 |
-7.64j |
10.04 |
-49.5 |
Экспериментальная проверка результатов расчета Для экспериментальной проверки расчета в целом необходимо к узлу D подключить источник напряжения, действующее значение и фаза которого равны вычисленным для напряжения UD, и проверить действующие значения токов и напряжений в схеме. Как видно из рис. 4.25, они совпадают с вычисленными. Шаг 9
Расчет и построение векторных диаграмм 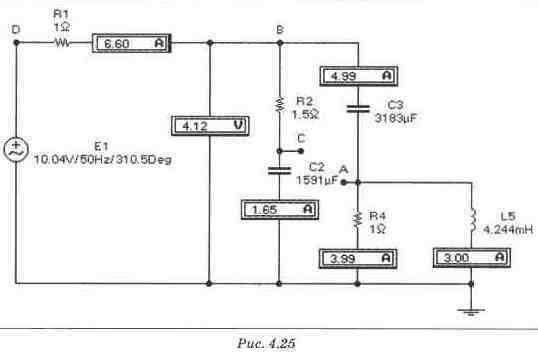
Текст из программы комплексного калькулятора с результатами ! 9. Вычисление полной мощности цепи в комплексной форме
 Векторные
диаграммы мощности построены в масштабе 1:10. Векторные
диаграммы мощности построены в масштабе 1:10.
|
Операция |
Real |
Imag |
Abs |
Arg, rp |
|
S=UD*&I1 |
63.8 |
-18.4j |
66.4 |
-16 |
Экспериментальная проверка результатов расчета Экспериментальная проверка результатов расчета проводится так же, как в задаче 1.
Векторные диаграммы тока, напряжения и мощности 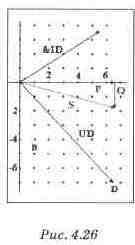
Задачи для самостоятельного решения 1, Простые схемы
Задачи, приведенные в файлах с4_11… С4_40, решаются подобно задаче 1, разобранной в разделе 4.2.
Задача 1 (с4_11) Определить комплекс тока через катушку индуктивности L2 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 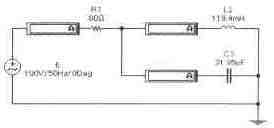
Задача 2 (с4_12) Определить комплекс тока через сопротивление R1 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 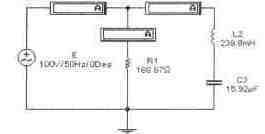
Задача 3 (с4_13) Определить комплекс тока через сопротивление R2 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 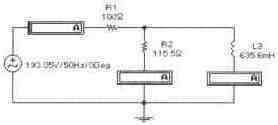
Задача 4 (с4_14) Определить комплекс тока через сопротивление R1 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 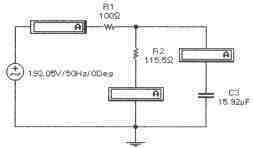
Задача 5 (с4_15) Определить комплекс напряжения на сопротивлении R3 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета.
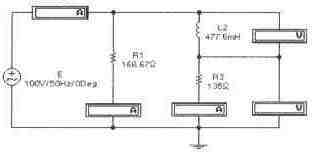
Задача 6 (с4_16) Определить комплекс напряжения на сопротивлении R2 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 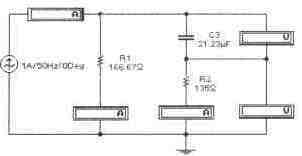
Задача 7 (с4_17) Определить комплекс тока через сопротивление R2 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 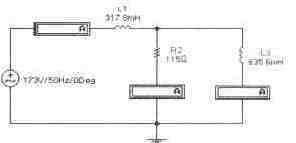
Задача 8 (с4_18) Определить комплекс тока через сопротивление R2 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 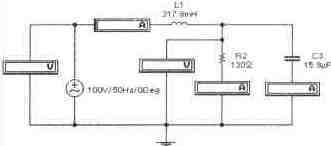
Задача 9 (с4_19) Определить комплекс тока через сопротивление R2 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 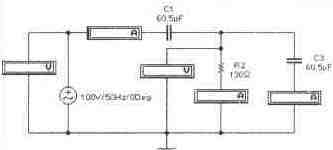
Задача 10 (с4_20) Определить комплекс тока через сопротивление R2 методом свертки-развертки. Рассчитать комплекс мощности, определить активную, реактивную и полную мощности цепи. Провести экспериментальную проверку результатов расчета. 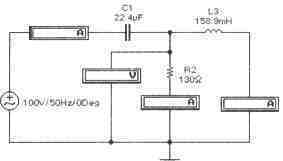
Задачи с4_21…с4_40 помещены на дискете, прилагаемой к книге.
2. Многоконтурные схемы
Задачи, приведенные в файлах с4_41… с4_70, решаются подобно задаче 2, разобранной в разделе 4.2. Все задачи отличаются лишь схемой и имеют общее задание: а) Рассчитать все необходимые комплексы и построить векторную диаграмму токов и топографическую диаграмму напряжений. б) Рассчитать полную S, активную Р и реактивную Q мощности цепи синусоидального тока. в) Построить на одном графике временные диаграммы зависимостей uвх(t), iвх(t), рвх(t). По результатам расчета указать на временной диаграмме pax(t) численные значения полной S и активной Р мощностей. г) Проверить экспериментально результаты расчета.
Задача 1 (с4_41) 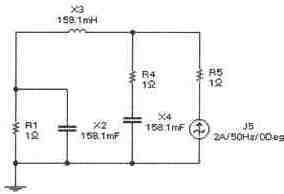
Задача 2 (с4_42) 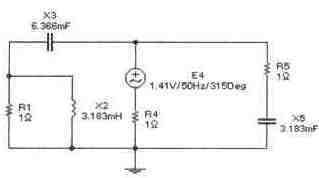
Задача 3 (с4_43) 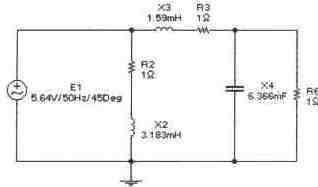
Задача 4 (с4_44) 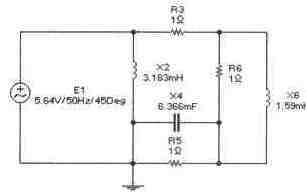
Задача 5 (с4_45)
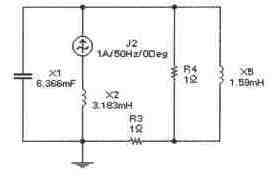
Задача 6 (с4_46) 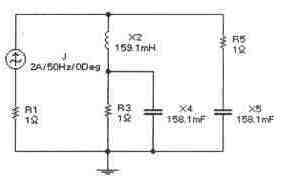
Задача 7( с4_47) 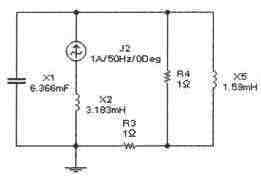
Задача 8 (с4_48) 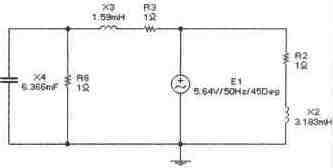
Задача 9 (с4_49) 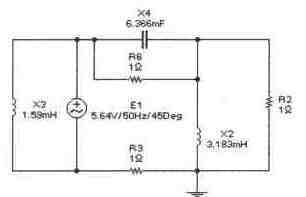
Задача 10 (с4_50) 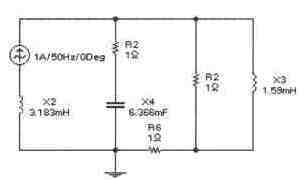
Задача 11 (с4 51) 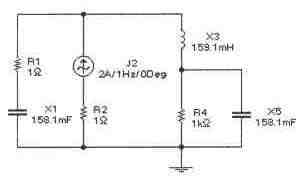
Задача 12 (с4_52) 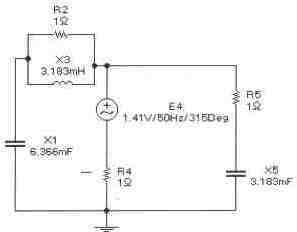
Задача 13 (с4_53) 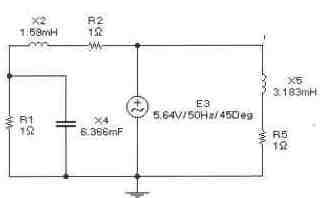
Задача 14 (с4 54) 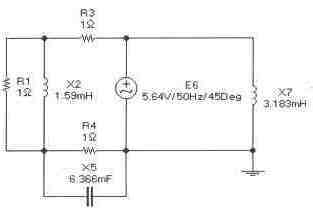
Задача 15 (с4_55) 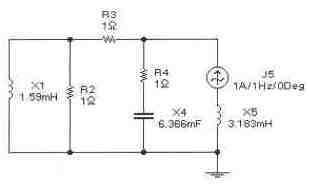
Задача 16 (с4_56) 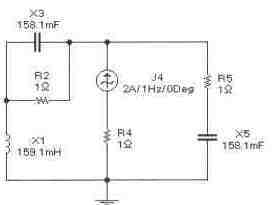
Задачи с 4_57…с 4_70 помещены на прилагаемой к книге дискете.
|







