6.5. Фильтрующие элементы
Фильтрующие элементы используются
в блоках питания для фильтрации сигналов, в качестве корректирующих звеньев
в системах управления и т.п. Фильтры делятся на два больших класса — пассивные
и активные, причем основным отличием активного фильтра является наличие усилительного
элемента — обычно это ОУ. Если в фильтре содержится один реактивный элемент
(емкость или индуктивность), то такой фильтр называется фильтром первого порядка,
если два — то второго порядка, и т.д.
Наиболее распространенным
пассивным фильтром первого порядка является интегрирующая RC-цепь, входящая
в состав рассмотренного выше интегратора, который может рассматриваться как
активный низкочастотный фильтр первого порядка. Этот же фильтр в технике электропитания
называется Г-образным, в аудиотехнике — фильтром нижних частот (ФНЧ), а в технике
управления — корректирующим или интегрирующим звеном [29]. Основными характеристиками
фильтра являются АЧХ и ФЧХ. Например, для интегрирующей цепи на рис. 10.22 они
описываются выражениями: 
Следует отметить, что фильтры
на базе RC-цепей обладают своеобразной дуальностью. Если на рис. 10.22 поменять
местами элементы R и С, то получим фильтр верхних частот (ФВЧ).
Классической схемой фильтра
второго порядка является последовательная RLC-цепь (рис. 10.23). Если выходной
сигнал измерять на конденсаторе, получим ФНЧ (его АЧХ показана на рис. 10.24),
а если на индуктивности L — ФВЧ.
Как видно из рис. 10.24,
RLC-цепь обладает явными резонансными свойствами, ее АЧХ и ФЧХ описываются выражениями: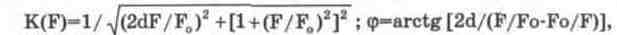 
где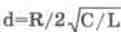 
— коэффициент затухания,
его обратная величина называется добротностью Q=l/d, часто определяемой как
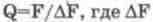— ширина полосы пропускания
по уровню 0,707 (-3 дБ);
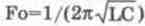— резонансная частота.
.
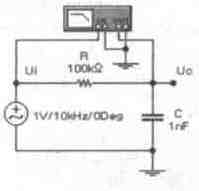
Рис. 10.22.
Схема пассивного ФНЧ первого порядка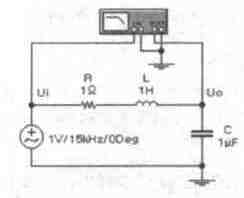 
Рис. 10.23.
Фильтр второго порядка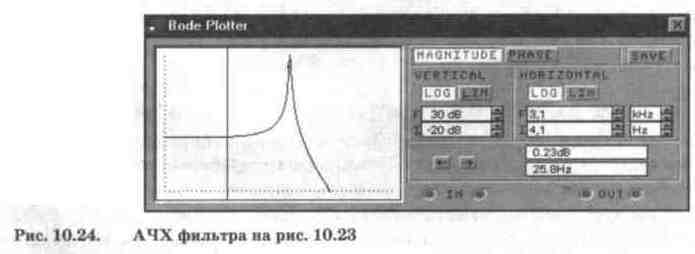 
При практической реализации
RLC-фильтров (особенно низкочастотных) наибольшие трудности возникают с изготовлением
катушек индуктивности, их экранированием, а при больших значениях индуктивности
— с проблемой массы и геометрических размеров. С появлением ОУ эти проблемы
решены с использованием активных ПС-фильтров. Появились так называемые безындуктивные
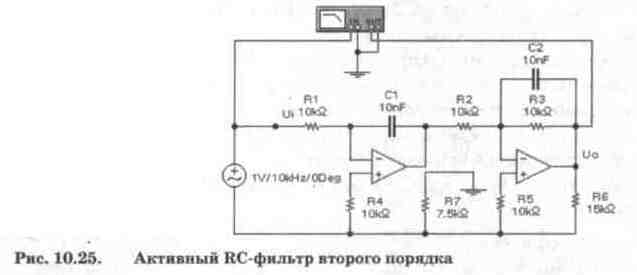
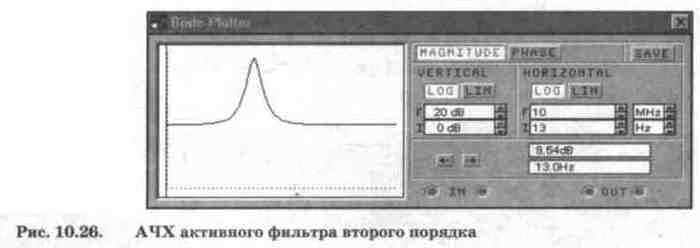
частотные фильтры. В качестве примера на рис. 10.25 приведена схема активного
ФНЧ второго порядка на ОУ [30], АЧХ которого показана на рис. 10.26.
Из полосовых фильтров наибольшее
распространение получили фильтры, АЧХ которых описывается полиномами Баттерворта,
Чебышева и Бесселя; для расчета таких фильтров применяются специальные таблицы
[31].
Фильтры Баттерворта. Эти
фильтры характеризуются максимально плоской АЧХ в полосе пропускания. Управление
величиной выходного напряжения и перестройка по частоте в широком диапазоне
осуществляются в этих фильтрах проще, чем
в других фильтрах, поскольку при каскадном соединении все секции настраиваются
на одну и ту же частоту.
Фильтры Чебышева. Эти фильтры
обеспечивают наивысшую крутизну АЧХ в переходной полосе частот. Однако при этом
АЧХ в полосе пропускания приобретает колебательный характер. Чем больше неравномерность
в полосе пропускания, тем выше крутизна затухания в переходной полосе частот.
Фильтры Бесселя. Фильтры
Бесселя обладают максимально плоской характеристикой группового времени запаздывания
(производная от ФЧХ по частоте) и линейностью ФЧХ в полосе пропускания. Однако
-Крутизна затухания фильтра невелика.
В каталоге схем программы
EWB имеется пример низкочастотного полосового фильтра (файл speech.са4) с полосой
пропускания от 300 Гц до 3 кГц. Фильтр представляет собой два последовательно
включенных фильтра четвертого порядка на ОУ (ФНЧ и ФВЧ). В каталоге имеются
также схемы активных избирательных ФНЧ на базе Т-образного моста (bass-amp.ca4)
и пропорционально-интегрирующий фильтр (riaa.ca4).
Контрольные вопросы и задания
1. По каким признакам классифицируются
фильтрующие элементы?
2. Для ФНЧ на рис. 10.22
проведите расчет АЧХ и ФЧХ в диапазоне частот 0,1… 100 кГц и сравните их с
результатами моделирования.
3. Для фильтра второго
порядка на рис. 10.23 рассчитайте АЧХ и ФЧХ в диапазоне частот 30… 300 Гц
и сравните их с результатами моделирования.
4. Проведите моделирование
активного RC-фильтра на рис. 10.25. Установить зависимость АЧХ фильтра от сопротивления
резисторов R2 и R3.
|
