Поиск по сайту

10.2. Универсальные функциональные преобразователи

Функциональными преобразователями или нелинейными решающими блоками называют устройства, воспроизводящие заданные нелинейные функции одного или нескольких аргументов. Кроме моделирующих устройств, они применяются для линеаризации датчиков (см. разд. 10.2) и в качестве корректирующих звеньев в автоматических системах управления для улучшения их динамических характеристик [29,65].

Функциональные преобразователи разделяются на универсальные и специализированные. Универсальные преобразователи позволяют с помощью одного устройства воспроизводить различные функциональные зависимости. Специализированные же преобразователи используются, как правило, для воспроизведения только одной определенной зависимости. Примерами специализированных преобразователей могут служить устройства, использующие квадратичные или логарифмические участки вольтамперных характеристик электронных приборов и т.п. К ним относятся также устройства для деления и перемножения сигналов, возведения в степень, имитаторы нелинейности звеньев автоматических систем управления.

При формировании нелинейной зависимости используется ступенчатая или кусочно-линейная аппроксимация. При этом исходные данные задаются в виде аналитической зависимости, которая при реализации может быть расчленена на элементарные математические операции; в виде графической зависимости; в виде семейства кривых, записанных каким-либо способом, а также в виде таблиц с указанием способа интерполяции между заданными точками.

Различают преобразователи разомкнутого и компенсационного (следящего) типа. Основные требования, предъявляемые к функциональным преобразователям, заключаются в следующем [29].

1. Функциональное преобразование должно выполняться над входными величинами, заданными в виде напряжений постоянного тока в диапазоне значений, допускаемых для используемых при этом операционных усилителей.

2. Входное сопротивление функционального преобразователя не должно быть ниже 10…50 кОм, выходное — не выше 10…20 Ом. Функциональный преобразователь должен обладать также достаточной выходной мощностью для удобства сопряжения с другими элементами.

3. Воспроизведение заданной функции должно быть выполнено с точностью не ниже 1…2% от полной шкалы.

4. Уровень шумов в выходном напряжении (постоянного тока) не должно превышать 5…10 мВ.

5. Функциональные преобразователи должны воспроизводить однозначные и неоднозначные нелинейные зависимости, а также нелинейные зависимости, приводимые к элементарным функциям и полученные в результате эксперимента.

6. Обеспечение возможности воспроизведения нелинейных зависимостей с малым и большим значением первой производной, а также немонотонных функций с большим числом экстремумов.

Из электронных функциональных преобразователей наибольшее распространение получили диодные преобразователи. Они представляют собой в большинстве случаев параметрические устройства, использующие кусочно-линейную аппроксимацию заданной функции.

Диодные функциональные преобразователи делятся на две группы. Первая группа представляет собой делители напряжения с переменным коэффициентом деления, вторая — решающие усилители с переменным коэффициентом передачи.

Схема преобразователя первой группы показана на рис. 14.5, а. Она содержит два одинаковых плеча, одно из которых (левое) формирует синтезируемую функцию в первом квадранте, а второе (правое) — в третьем. Каждое плечо схемы (далее используются обозначения только для левого плеча) содержит делитель опорного напряжения Uop на резисторах R01 — R04, три диода VD1…VD3 с последовательно включенными резисторами R1…R3. Выходной сигнал преобразователя Uo подается на вход канала А осциллографа, а входной Ui — на вход канала В и вход преобразователя. В качестве источника входного (испытательного) сигнала используется функциональный генератор, режимы работы которого показаны на рис. 14.5, а.

Формируемая преобразователем функция Uo=f(Ui) (рис. 14.5, в) содержит две ветви (в первом и третьем квадрантах); они полностью идентичны вследствие симметрии плеч схемы на рис. 14.5, а. Каждая ветвь имеет три излома, что соответствует использованию трех цепочек из последовательно включенных диода и резистора.

Формирование функциональной зависимости Uo=f(Ui) происходит следующим образом (на примере левого плеча). С помощью делителя на резисторах R01…R04 и источника опорного напряжения Uop на катодах диодов VD1…VD3 формируются запирающие напряжения U01, U02, U03, равные 5, 10 и 15 В соответственно. В исходном состоянии Ui=0 и все диоды заперты. Когда Ui начинает увеличиваться, формируется первый (начальный) участок зависимости, при этом выходное напряжение изменяется в соответствии с выражением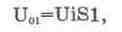

(14.16)

где Si=Rn/(Rn+R) — крутизна первого участка.

Поскольку в нашем случае Rn>>R, то S1=l и Uo1=Ui. Заметим, что при определении сопротивления нагрузки необходимо учитывать также сопротивление, определяемое током утечки обратно смещенных диодов, если оно соизмеримо с сопротивлением резистора R.

Когда Ui достигает значения U01+Ud (Ud — падение напряжения на открытом диоде, примерно равное 0,6 В), открывается диод VD1 и начинается формирование второго участка кривой, при этом выходное напряжение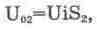

(14.17)

где S2=Re1/(Re1+R) — крутизна второго участка; Rе1=R1+Rd+RO¦¦(R02+R03+R04);

¦¦ — значок параллельного включения резисторов; Rd — сопротивление открытого диода VD1.

Когда Ui достигает значения U02+Ud открывается диод VD2 и начинается формирование третьего участка кривой в соответствии с выражением: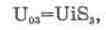

(14.18)

где S3=Rez/(Re2+R) — крутизна третьего участка.

Выражение для Re2 в рассматриваемом случае получается значительно сложнее, чем для Re1. Обычно на практике сопротивления резисторов R1…R3 выбираются достаточно большими, чтобы можно было пренебречь сопротивлением делителя опорного напряжения и сопротивлением открытого диода. И дело здесь не только в упрощении расчетов, но и в затруднении получить, например, точное значение сопротивления открытого диода, являющейся функцией проходящего через него тока. Если пренебречь влиянием указанных сопротивлений, то для второго и третьего участков будем иметь

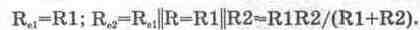(14.19)

Аналогичным образом формируется и четвертый участок синтезируемой зависимости. Заметим, что каждый следующий участок зависимости Uo=f(Ui) служит продолжением предыдущего, являясь своеобразным "пьедесталом" для формирования нового участка и обеспечивая тем самым непрерывность аппроксимируемой функции.

Из рис. 14.5, а нетрудно видеть, что с увеличением выходного напряжения Uo приращения входного Ui уменьшаются. Поэтому такой преобразователь принято называть преобразователем для воспроизведения функции с убывающей производной (выпуклая кривая). Для формирования функций с возрастающей производной (вогнутая кривая) все диоды преобразователя в исходном состоянии должны быть открыты, т.е. для реализации такого преобразователя достаточно изменить полярность включения диодов или полярность источника опорного напряжения. При изменении входного напряжения будут поочередно закрываться диоды, что будет вызывать увеличение крутизны при срабатывании очередного по порядку диода и, следовательно, преобразователем будет формироваться функция с возрастающей производной. Очевидно, что для такого преобразователя будут справедливы изложенные выще результаты анализа для схемы на рис. 14.5, а.

Из проведенного анализа видно, что для разработки функционального преобразователя рассмотренного типа необходимо:

О разбить заданную, например, в виде графика функцию на требуемое количество участков аппроксимации по оси Uo, при этом будут получены соответствующие

значения Uo на каждом участке (узлы аппроксимации

О по полученным значениям Uon рассчитать делитель опорного напряжения с учетом падения напряжения Ud на открытом диоде из условия, что ток через делитель равен 50…100 мА (для схемы на рис. 14.5, а он равен 20/400=0,05 А=50 мА), при этом на выходах делителя должны быть получены опорные напряжения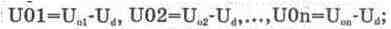

О по полученным в п. 1 разбиениям заданной функции определить приращения на каждом участке аппроксимации, соответствующие выбранным значениям Uo;

О для каждого участка аппроксимации заданной зависимости определить крутизну, т.е.

О задавшись сопротивлением резистора R в пределах 30… 50 кОм и используя формулы (14.16) — (14.19) и полученные в п. 4 значения крутизны для каждого участка, рассчитать значения сопротивлений

Как видно из анализа схемы диодного преобразователя на рис. 14.5, а, они просты по устройству и легко могут быть подстроены в процессе наладки (после проведения ориентировочных расчетов), что позволяет достичь точности воспроизведения заданной функции до десятых долей процента от ее максимального значения [61]. Основными недостатками таких преобразователей является ограниченный динамический диапазон по выходному напряжению (по сравнению с входным), что накладывает ограничения при воспроизведении немонотонных функций, а также сильная зависимость точности воспроизведения от нагрузки.

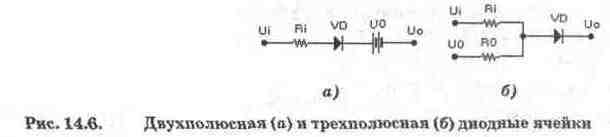
Более совершенными являются диодные функциональные преобразователи, реализующие метод решающего усилителя с переменным коэффициентом передачи. В таких преобразователях чаще всего используются диодные ячейки, показанные на рис. 14.6. Двухполюсная ячейка (рис. 14.6, а) отличается простотой расчета и последующей настройки, однако для каждой такой ячейки требуется незаземленный источник опорного напряжения UO. Для трехполюсной ячейки (рис. 14.6, б) источник опорного напряжения UO общий для всех ячеек, необходимое запирающее (или отпирающее) напряжение на диоде VD формируется с помощью резисторов RO и Ri, которые одновременно используются и при формировании крутизны моделируемой функции на соответствующем участке аппроксимации. Это обстоятельство создает определенные трудности при расчетах и последующей экспериментальной подстройке.

При построении рассматриваемых преобразователей используются в различных комбинациях схемы на рис. 14.7. Если принять, что для данного участка воспроизводимой функции сопротивление соответствующей диодно-резистивной ячейки равно Rd1 а для схемы на рис. 14.7, в — Rd1 и Rd2, то крутизна формируемого участка (коэффициент передачи суммирующего усилителя) для схем на рис. 14.7, а, б, в

соответственно составит: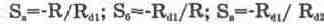

. Знак - указывает на инвертирующие своства суммирующего усилителя.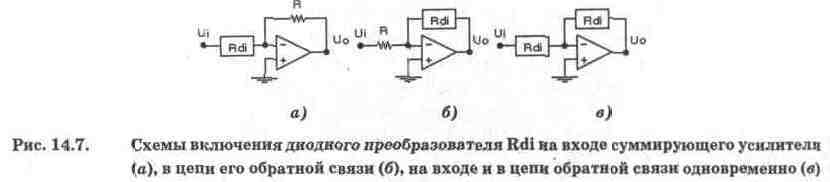

В качестве примера рассмотрим функциональный преобразователь с двухполюсными диодными ячейками, схема которого приведена на рис. 14.8, а. Преобразователь содержит два идентичных набора из трех двухполюсных диодных ячеек с опорными (запирающими) напряжениями 5,10 и 15 В (как и в схеме на рис. 14.5, а). Начальный участок моделируемой функции (до срабатывания диодов VD1 или VD1') формируется с помощью резистора RO. В положении "сдвоенного" переключателя X, показанном на схеме и управляемого клавишей Х клавиатуры, преобразователь реализует схему включения на рис. 14.7, а; при переводе этого переключателя в другое (противоположное) положение — схему на рис. 14.7, б. Суммирующий усилитель выполнен на операционном усилителе OU1, на OU2 выполнен инвертирующий усилитель с коэффициентом передачи -1. В положении ключа Z, показанном на схеме рис. 14.8, а, моделируемая знакопеременная функция имеет вид, показанный на рис. 14.8, б. При переводе ключа Z одноименной клавишей клавиатуры в другое положение моделируемая функция имеет вид, показанный на рис. 14.8, в.

Из сравнения кривых на рис. 14.8, б и 14.8, в видно, что они абсолютно идентичны, но располагаются в различных квадрантах. Из схемы преобразователя видно, что достигается это использованием инвертирующего усилителя на OU2: в первом случае (рис. 14.8, б) выходной сигнал преобразователя снимается с выхода OU2, а во втором (рис. 14.8, в) — с выхода OU1.

Теперь вернем переключатель Z в исходное состояние (показанное на рис. 14.8, а), а переключатели Х одноименной клавишей переведем в другое положение. Для этого случая моделируемая функция показана на рис. 14.8, г.

Из сравнения функций на рис. 14.8, б и 14.8, г видно, что эти функции отличаются не только крутизной участков аппроксимации, но и характером производной: в первом случае она возрастающая, а во втором — убывающая. Из схемы преобразователя видно, что такой эффект достигается за счет включения собственно диодного преобразователя на входе решающего усилителя на OU1 (реализуется схема на рис. 14.7, а) или в цепь его отрицательной обратной связи (реализуется схема на рис. 14.7, б).

Во всех рассмотренных режимах работы преобразователя на рис. 14.8, а формирование начального (нулевого) участка производится с помощью резисторов R и RO, т.е. крутизна этого участка равна So=R/RO вплоть до момента срабатывания диода VD1 (или VD1'). Однако из-за сравнительно большого сопротивления последовательно включенного с этим диодом резистора R1=10 кОм и существенной нелинейности начального участка вольтамперной характеристики диода процесс его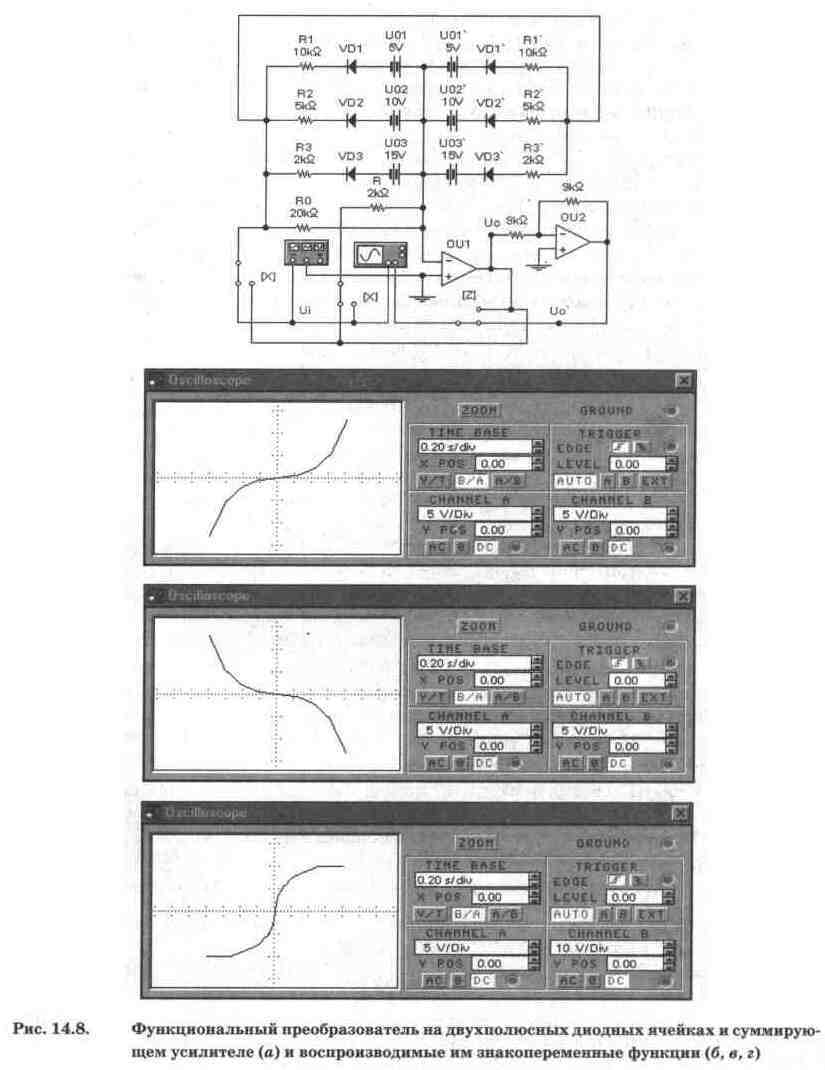

переключения затягивается. Это явление удобно наблюдать в увеличенном масштабе в режиме ZOOM осциллографа. Кривая на рис. 14.8, б в таком режиме показана на рис. 14.9, из которого видно, что первый излом функции наблюдается при Ui=Tl=5,6 В (в этой точке установлена визирная линейка 1), а второй излом — при Ui=T2=10,35 В (визирная линейка 2), т.е. с увеличением тока через диод (за счет уменьшения сопротивления последовательно включенного с ним резистора) напряжение его срабатывания как бы уменьшается. Однако это можно трактовать и по-другому. Когда входное напряжение достигает опорного уровня, например, U01=5 В, диод VD1 приоткрывается и начинается процесс шунтирования резистора RO сопротивлением Rl+Rd(Ui). Когда напряжение Ui незначительно превышает опорное напряжение U01, рабочая точка диода находится на пологом участке характеристики и его сопротивление Ra(Ui)>Rl. С увеличением Ui увеличивается ток через диод и уменьшается Ra(Ui), однако за счет одновременного увеличения падения напряжения на резисторе R1 этот процесс замедляется. Такое "топтание на месте" за счет существенной нелинейности начального участка вольтамперной характеристики диода и вызывает наблюдаемую задержку в формировании очередного участка аппроксимации. При этом с уменьшением сопротивления последовательно включенного с диодом резистора время "топтания на месте", естественно, уменьшается, что мы и наблюдаем на рис. 14.9.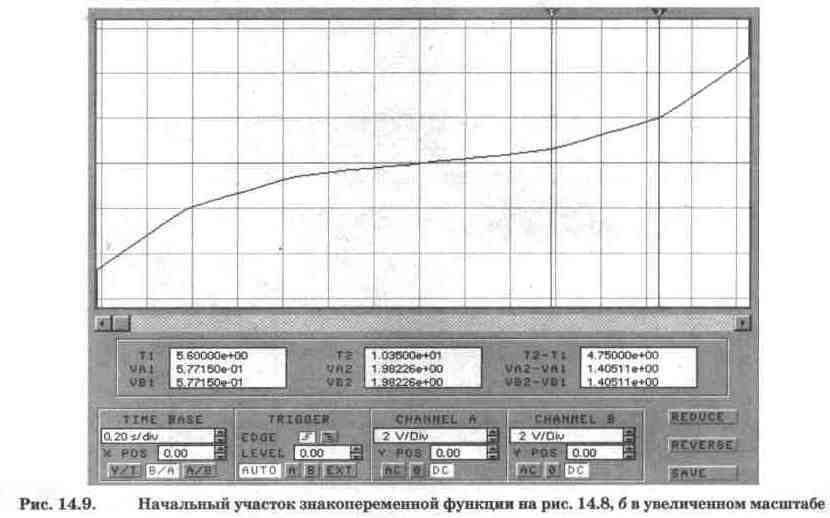

Из имеющихся в программе EWB библиотечных компонентов в качестве универсального функционального преобразователя может быть использован управляемый полиномиальный источник (в дальнейшем — блок), выходной сигнал которого описывается полиномом следующего вида (см. гл. 4):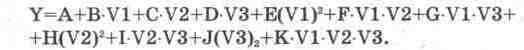

Коэффициенты полинома А…К задаются с помощью диалогового окна. Например, для случая преобразователя с квадратичной передаточной характеристикой, схема которого показана на рис. 14.10, параметры диалогового окна имеют значения, приведенные на рис. 14.11.

Как следует из рис. 14.10, источник входного сигнала подключен ко входу 1 преобразователя, т.е. в вышеприведенной формуле Vl=Ui. В таком случае на основании данных окна (рис. 14.11) выражение для выходного напряжения модели может быть записано в следующем виде:

(14.20)

Постоянная А в диалоговом окне задается в вольтах, входное напряжение (см.

лицевую панель генератора на рис. 14.10)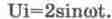

Учитывая известное из тригонометрии выражение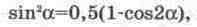

из (14.20)получаем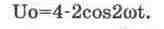

Результаты моделирования рассматриваемого преобразователя показаны на рис. 14.12, откуда видно, что на выходе преобразователя действительно формируется сигнал в соответствии с выражением (14.21).

Передаточная характеристика преобразователя (рис. 14.13) действительно имеет квадратичный характер, однако ее изображение искажено. Искажения носят гистерезисный характер и объясняются дрожанием фазы колебаний функционального генератора, поскольку формирование передаточной характеристики происходит в течение нескольких периодов его колебаний. В связи с этим была разработана модель генератора одиночного треугольного сигнала, оформленная в виде подсхемы gen1 (рис. 14.14, а).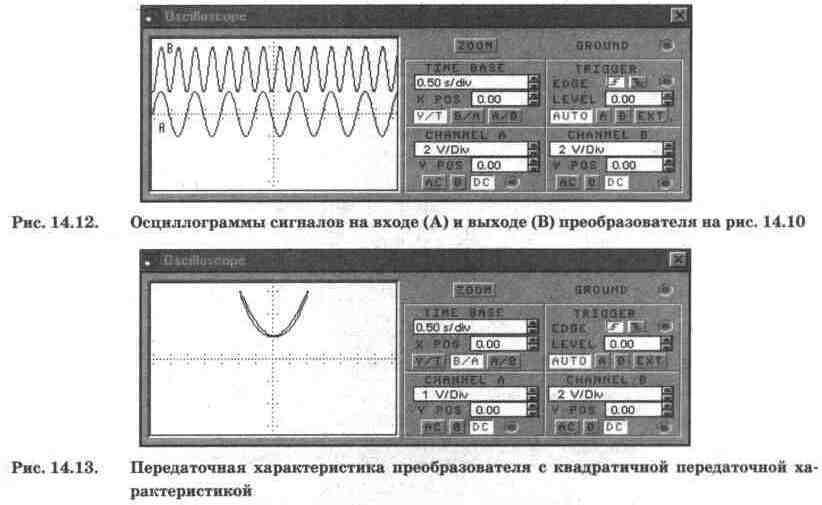

Генератор выполнен на базе интегратора, двух источников постоянного напряжения Ul, U2 и программно управляемых переключателей 1, 2, 3 из библиотеки Control, параметры которых с помощью диалогового окна выбраны следующим образом: время включения Топ=0 для всех переключателей, время выключения Toff выбрано равным 2, 6 и 8 с соответственно для переключателей 1, 2, и 3. В момент t<0 (перед пуском) все переключатели находятся в положении, показанном на рис. 14.19, в момент пуска (t=0) все переключатели переводятся в противоположное положение, при этом ко входу интегратора оказывается подключенным источник напряжения U2 положительной полярности и на его выходе начинает формироваться первая половина отрицательной полуволны треугольного сигнала (см. осциллограмму на рис. 14.14, б). Поскольку источник напряжения U2 подключается ко входу интегратора на время 2с, то за это время напряжение на его выходе достигает значения Uo=:tU2/RC=2•2/106•10-6=4 В, что совпадает с амплитудным значением на осциллограмме. В момент t=2 с переключатель 1 возвращается в исходное состояние и ко входу интегратора на время 4 с подключается источник отрицательного напряжения U2, после чего начинается формирование второй половины отрицательной полуволны и первой половины положительной полуволны. Нетрудно подсчитать, что амплитуда положительной полуволны также будет равна 4 В. В момент t=6c ключ 2 переводится в исходное состояние и ко входу интегратора на время 2 с подключается источник напряжения U2, в результате чего формируется вторая половина положительной полуволны выходного сигнала. В момент t=8 с формирование периода треугольного сигнала заканчивается и выход интегратора переключателем 3 подключается к общей шине (заземляется).

Результаты моделирования преобразователя на рис. 14.10 (при А = 0) с использованием рассмотренного генератора вместо функционального генератора показаны на рис. 14.15, из которого видно, что искажения изображения характеристики отсутствуют.

В заключение рассмотрим преобразователь с кубичной передаточной характеристикой (рис. 14.16, а). Преобразователь содержит два полиномиальных блока Р1 и Р2. В первом блоке реализуется рассмотренная выше квадратичная функция (при А=0), а во втором — функция перемножения входного сигнала Ui и выходного сигнала первого блока (для Р2 выбрано А=0 и F=1, см. рис. 14.11). Таким образом, для этого преобразователя Uo=(Ui)3. В качестве источника испытательного сигнала используется рассмотренный выше генератор genl. Передаточная характеристика преобразователя показана на рис. 14.16, б.

Таким образом, на базе управляемого полиномиального источника напряжения (блока) можно создавать разнообразные функциональные преобразователи для моделирования элементов систем автоматического управления (к сожалению, их нельзя встраивать в реальные системы).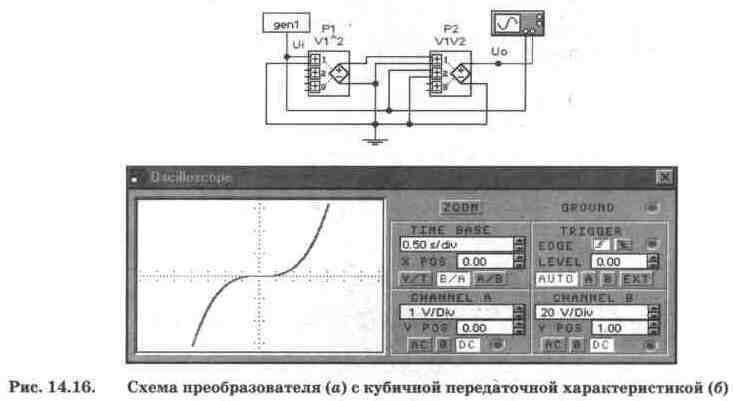

Следует отметить, что наличие в системе регулирования звена с квадратичной или кубичной характеристикой приводит к увеличению коэффициента усиления с увеличением входной величины. В одноконтурных системах регулирования это может привести к сужению области устойчивости системы, способствуя возникновению расходящихся колебаний при больших начальных отклонениях там, где чисто линейная система была бы устойчивой. В многоконтурных системах звено с квадратичной или кубичной характеристикой может оказаться полезным. Звенья с такими характеристиками иногда специально вводят в дополнительные обратные связи регулятора для улучшения качества процесса регулирования. Например, увеличение коэффициента обратной связи в регуляторе при больших отклонениях с помощью звена с кубичной характеристикой (в отличие от увеличения коэффициента усиления прямой цепи регулятора) может способствовать подавлению колебаний в процессе регулирования и расширению области устойчивости.

Контрольные вопросы и задания

1. Дайте определение функционального преобразователя и области его "использования.

2. Приведите краткую классификацию функциональных преобразователей и перечислите предъявляемые к ним требования.

3. Какие принципы используются при построении диодных функциональных преобразователей?

4. Составьте аналитическое выражения для расчета четвертого участка аппроксимации функции на рис. 14.5, в.

5. Можно ли использовать преобразователь на рис. 14.5, а для воспроизведения знакопеременной функции с возрастающей производной?

6. Составьте формулы для определения крутизны каждого участка аппроксимации преобразователя на рис. 14.8, а. Сопротивлением диодов Rd пренебрегите, крутизну начального участка примите равной So=R/RO.

7. Составьте схему преобразователя с квадратичной передаточной характеристикой с использованием двух полиномиальных блоков и проведите ее моделирование. Полученные результаты сопоставьте с результатами на рис. 14.15.

8. Составьте схему преобразователя с кубичной передаточной характеристикой с использованием трех полиномиальных блоков. Результаты моделирования сопоставьте с результатами на рис. 14.16, б.