2.4. Резонансные цепи
Явление,
при котором индуктивное и емкостное сопротивления в RLC-цепи равны, называется
резонансом.
Различают
последовательный (для последовательной RLC-цепи) и параллельный (для параллельной
RLC-цепи) резонанс. Последовательную RLC-цепь чаще всего называют последовательным
колебательным контуром, а параллельную RLC-цепь — параллельным колебательным
контуром. В случае малых потерь (сопротивление R пренебрежимо мало) для обоих
контуров резонанс наступает при условии
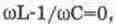
откуда
получается широко известное выражение для резонансной частоты;
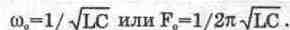 (6.4). (6.4).
При
последовательном резонансе (для последовательного контура) ток в цепи на рис.
6.5 определяется только сопротивлением R и совпадает по фазе с напряжением
входного сигнала. При этом ток в цепи равен I„=U„/R и напряжения на индуктивности
LT¦ и конденсаторе Uc
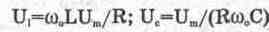 (6.5) (6.5)
могут
превышать напряжение входного сигнала в Q раз. Безразмерная величина
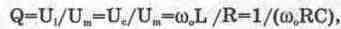 (6.6) (6.6)
называемая
добротностью, показывает, во сколько раз напряжение на индуктивности или емкости
при резонансе превышает входное напряжение контура. На практике используется
также величина, обратная добротности, которая называется коэффициентом затухания
d=l/Q. Из (6.6) видно, что добротность контура возрастает с увеличением индуктивности
L и уменьшением сопротивления потерь R и емкости С контура.
С
учетом (6.4) выражение (6.6) может быть записано также в виде Q=W/R, где
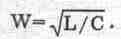 (6.7) (6.7)
Параметр
W имеет размерность сопротивления и называется характеристическим сопротивлением
контура.
Амплитудно-частотная
характеристика резонансной цепи определяется как отношение тока, определяемого
выражением (6.2), к току при резонансе, т.е.
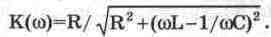 (6.8) (6.8)
В
радиотехнике зависимость, описываемую выражением (6.8), обычно называют резонансной
кривой и для малых отклонений частоты относительно резонансной частоты используют
для нее приближенное выражение:
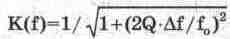 (6.9) (6.9)
где
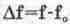 — расстройка по частоте. — расстройка по частоте.
Приведем
пример расчета последовательной RLC-цепи (рис. 6.10). Согласно (6.4) при указанных
на схеме значениях индуктивности и емкости
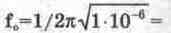 159,155
Гц, что соответствует частоте входного сигнала, т.е. в цепи имеет место резонанс
токов. 159,155
Гц, что соответствует частоте входного сигнала, т.е. в цепи имеет место резонанс
токов.
Значение
тока в цепи I„,=U„¦/R= 1/1000=1 мА соответствует показаниям амперметра !„,.
Согласно
(6.5) падение напряжения на индуктивности и емкости U,=1000 0,001 1=1 В, U^O.OOl/OOOO/lO6)^
В.
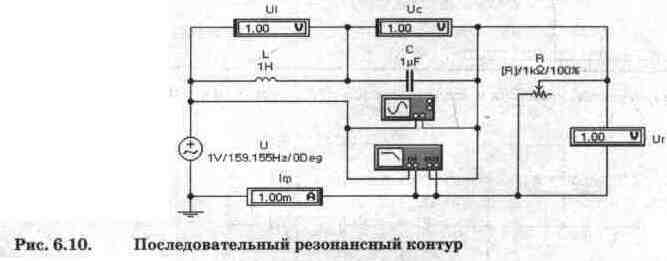
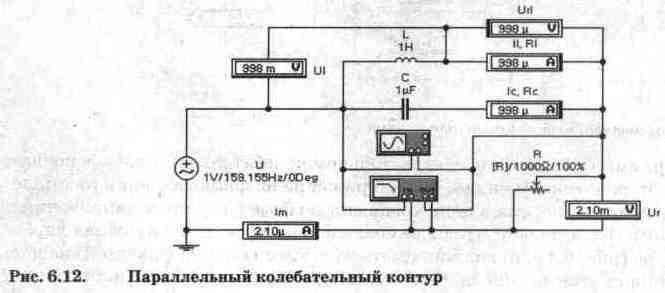
Осциллограммы
сигналов в последовательном колебательном контуре показаны на рис. 6.11, а,
из которого видно, что напряжение на сопротивлении (осциллограмма А) и, соответственно,
ток в цепи совпадает по фазе с входным напряжением (осциллограмма В). Это
означает, что на резонансной частоте фазо-частотная характеристика контура
(рис. 6.11, б) должна иметь нулевое значение. Однако из-за дискретности визирная
линия могла быть установлена на ФЧХ только вблизи резонансной частоты (161
Гц), поэтому значение фазы составляет 3,4°.
Рассмотрим
резонанс токов в параллельной RLC-цепи. Наибольшее внимание резонансу этого
типа уделяется в радиотехнике, где параллельный колебательный контур является
основным элементом большинства частотно-избирательных устройств. В теоретических
основах радиотехники показывается [51], что характеристики параллельного колебательного
контура можно рассчитывать по формулам для последовательного контура. Однако
имеются отличия, которые будут отмечены при рассмотрении конкретной схемы
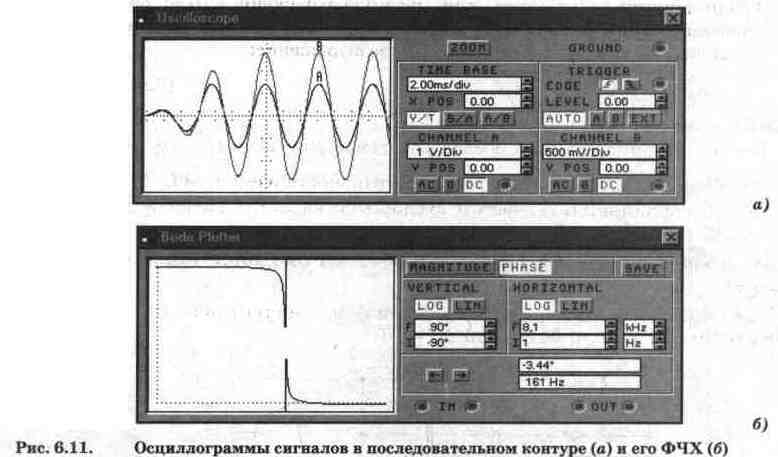
параллельного контура (рис. 6.12).
Собственно колебательный
контур состоит из двух параллельно включенных ветвей: индуктивной с сопротивлением
потерь в виде внутреннего сопротивления R¦ амперметра I, и емкостной с сопротивлением
потерь в виде внутреннего сопротивления Re амперметра 1с. Напомним, что эти
сопротивления могут изменяться и для рассматриваемой схемы установлены равными
1 Ом для обоих амперметров. К контуру подключены измерительные приборы, назначение
которых очевидно; например, вольтметры U, и U,, предназначены для измерения
падения напряжения на индуктивности L и на резисторе R.
Для
параллельного колебательного контура вводится параметр, который равен сопротивлению
контура на резонансной частоте и называется резонансным сопротивлением Rp,
определяемым по формуле:
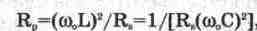 (6.10) (6.10)
где
R.=Rl+Rc — суммарное сопротивление потерь контура.
Соотношение
между подводимым к контуру током 1„ и током в контуре Ii, на резонансной частоте
определяется выражением:
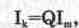 (6.11) (6.11)
где Q определяется выражением
(6.6), но с учетом того, что сопротивление потерь теперь обозначается как
R.. Для схемы на рис. 6.12 имеем: Z„.=(1000 1)72=500000 Ом; Q=(1000 1)/2=500.
Подводимый к контуру ток и ток контура: I„,=U/(Rp+R)=l/(500000-HOOO)=l,996
мкА; Ii,=l, 996-500=998 мкА, что практически совпадает с показаниями приборов.
Имеющие место неточности определяются приближенностью используемых формул.
Например, для параллельного контура точное значение резонансной частоты может
быть определено из выражения:
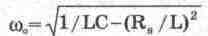 (6.11) (6.11)
В
случае пренебрежения сопротивлением R. выражение (6.11) совпадает с (6.4).
Из (6.11) видно, что с увеличением потерь контура R. его резонансная частота
уменьшается.
Амплитудно-частотная
характеристика параллельного контура рассчитывается с помощью выражения (6.8).
Для схемы на рис. 6.12 она имеет вид, показанный на рис. 6.13, а.
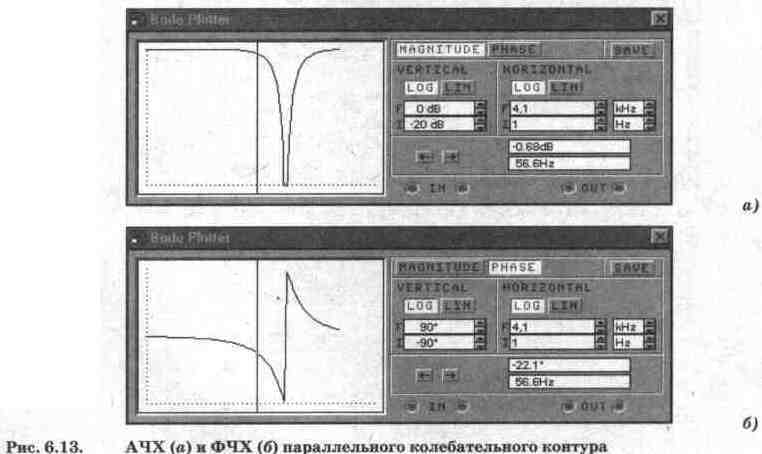
Фазо-частотная
характеристика параллельного колебательного контура рассчитывается с помощью
выражения (6.3) и показана на рис. 6.13, б.
Поскольку
для практических применений наибольший интерес представляет область частот
вблизи резонансной (в полосе 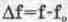 , где f — текущее значение частоты), то для удобства интерпретации
полученных результатов целесообразно использовать приближенную формулу для
ФЧХ в виде , где f — текущее значение частоты), то для удобства интерпретации
полученных результатов целесообразно использовать приближенную формулу для
ФЧХ в виде
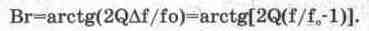 (6.12) (6.12)
Из
(6.12) видно, что при f=f„ фазовый угол равен нулю, однако уже при незначительном
отклонении частоты в одну или другую сторону от резонансной будет наблюдаться
резкое изменение фазы как в область отрицательных (при f<f„) так и положительных
значений (при f>f„). Причем, крутизна переходного участка тем больше, чем
больше добротность контура, а его ширина определяется отношением f„/Q, определяющем
полосу пропускания  на уровне 0,707 (это значение получается
после подстановки в выражение (6.9) значения на уровне 0,707 (это значение получается
после подстановки в выражение (6.9) значения 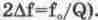
Контрольные
вопросы и задания
1.
Дайте определения явления резонанса в электрических цепях переменного тока
и назовите условия его возникновения. В каких областях техники резонансные
явления находят наибольшее применение?
2.
Для схемы на рис. 6.12 проведите расчеты и моделирование при сопротивлениях
потерь Rl=Rc=8 Ом. Уточните значение резонансной частоты с помощью соотношения
(6.11).
3.
Используя формулы (6.8), (6.3) и значения параметров на рис. 6.12, рассчитайте
амплитудно-частотную и фазо-частотную характеристики и сравните полученные
результаты с данными моделирования, приведенными на рис. 6.13.
|







